I was lucky enough to pose some interesting questions to Eng S Jama. He is an experienced electronics engineer turned author/tutor. Eng S Jama created a series of books portraying fractions visually. All this in an effort to help children understand and enjoy the basic maths concepts like fractions, decimals and percentages.
 1. What inspired this ‘out-of-the-box’ approach to this concept that so many children find boring, if not difficult.
1. What inspired this ‘out-of-the-box’ approach to this concept that so many children find boring, if not difficult.
I have been in education since 2009, from primary schools to secondary school/sixth form to further education colleges and I have observed how some children and even grown-ups struggle with basic maths fractions.
Example 1
I would ask a child to write a half or one-half, once I see them mixing up numbers.
They would write, 1÷2, , ½ or something similar. So far, so good.
Then, I would ask them to show what one and a half or one-and-half looks like.
They would write, 1÷2, , ½ or something very close to it. Yes, exactly the same as before!
If I mention that this new fraction is the same as one-half, some children would say, “Yes”.
“But, here is the 1 (pointing to the numerator) and there’s the half (i.e the denominator)”, they explain.
A few might even add, “What else do you want?”
Meaning, ‘You have or I’ve shown you the 1 and a half’. One-and-half. That’s it, sir.
The same goes for a quarter, third, fifth, sixth, eighth, tenth and so on.
Then I had realised how deep the problem with fractions is.
After that, I started sketching and scribbling in children’s exercise books, notepads and on loose sheets of paper.
Next, I converted those sketches and scribbles into handouts and worksheets.
But still, this was not enough.
Example 2
This is the brief story at the beginning of some of the books, Understanding Fractions Visually series.
In one evening, a friend of mine picked up her 3 children from school.
On the way home, she bought a pizza for the children.
Mum divided the pizza like this:
But the younger boy was NOT happy!
Here he is, very cross! “That is NOT fair!”, he yelled.
The problem is, he thought his older brother had more pizza! Two small slices versus one big slice.
Mum explained that all three children had the same amount of pizza.
But the younger boy would not accept and even tried to start crying.
Then, my friend and I suggested that the boys swap their pizzas, to which they agreed.
Then, the younger boy WAS happy!
This is when the idea of converting those notes and worksheets into full books hit me really hard.
The rest is history, as they say.
2. You say in your article, people use fractions in their daily life. Except for things like dividing a cake or pie on a special occasion, which other practical uses for fractions could you mention?
Everyday uses of fractions (percentages, ratio) include:
- Time
- Money
- Taxes
- Measurements
- Making, Designing … Things
- Probability, forecasts, gambling, games
- Clothing and footwear
- Food, drinks, medicine
- And many others.
We divide time into fractions in the form of centuries, years, seasons, months, weeks, parts of the day (dawn … sunrise, morning … noon … afternoon … evening … dusk, night, midnight) or day-time/night-time, hours, minutes and seconds.
In money, all the currencies (especially coins) in the world have denominations which are fractions of their unit currencies!
For example, £1 = 50p x2, 20p x5, 10p x10, 5p x20, 2p x50 and 1p x100.
In taxes, fractions (inc decimals and percentages) are used for income tax, stamp duties, shares, NINO contributions, excise duties (alcohol/tobacco/cigarette) motor/road tax and export/import taxes like those tariff wars now in place between the US and other countries/nations. Or the international trade tariffs that will kick in after Brexit.
Also, VAT, local council tax/poll tax, corporation tax, capital gains, inheritance (shared among beneficiaries/siblings)/inheritance tax and more.
Investments, interest rates, income/expenditure, promotions, remunerations/wages/salaries, shares & dividends, business rates, selling/buying (eg Sale! Save 25%, half-price, 1/3 off, buy 1 get 2nd for x% off), profit & loss, price increases/reductions (say against inflation), wills, charity/almsgiving, pensions, insurance and so on.
In SI measurements, we use fractions of a meter (m, cm, mm) for length and distance, fractions of a litre (l, cl and ml) for volume and capacity, and fractions of a kg/multiples of a gram (g, kg, tonne) for weight and mass.
Similarly, in Imperial units, inch, foot and yard are fractions of a yard. Also, ounce, pound and stone; fluid oz, pint and gallon etc. A yardstick is measured in fractions of a yard, Imperial tape measures, rulers and rules in fractions of a foot (sometimes fractions of an inch, foot and yard such as a carpenter’s tape measure).
Making and designing things.
Depending on application, a mortar mix can contain 3-part cement, 2-part sand and 1-part lime, or 1-part cement, 2-part sand and 1-part other material/s, and concrete 1-cement : 2-sand : 3-gravel.
Odds in sports, weather humidity %, the chance of rain etc, probability of team A, player B, political party C winning/losing, winning the National Lottery,
Cooking recipes use fractions.
½ tsb salt, ¼ tbsp oil, ¾ kg flour, 250ml water …
A cup of tea or coffee etc
x ml water, y ml milk… 3 tsb sugar, z g tea/a teabag…
Measuring jugs, beakers, measuring cups, scoops (for medicine, washing powder) and other containers in the kitchen often have fractions measurements or ‘graduations’. For instance, 1/4l, 1/2l, 3/4l, 1l or 1/4 pint, 1/2 pint, 3/4 pint, 1pint and so on.
Mixed or juice drinks
1½l water, ¾l lemon juice, ½ apple, 1 mango …
Care labels for garments eg 65% polyester, 35% cotton.
Shoe sizes – UK 7 (5½”); 8½” (21.5cm)…
Fruit + Fibre cornflakes; 5% fruit, rest other stuff.
Olive Oil spread; 21% olive oil, 79% blends of other oils.
% fat, % salt, % sugar, % alcohol, % active ingredient of substance/element/drug D, % body burn…
Solutions/compounds; Car washer fluid mix = 25% screenwash/75% water for normal driving conditions, or 50% screenwash/50% for winter.
Formulas in maths, science, engineering – ½ base x height, ½mc2 …
Even lessons/lectures/presentations, debates, TV programmes (programme schedule), everyday activities (x time for work, y time for this, z time for that), books (i.e chapters), surveys, opinion polls/elections (% satisfied, % female, % agreed, % voted for this political party) are based on fractions … In fact most things in life, I would say.
3. Would you agree that a more creative approach to Maths is much needed in our education system?
Yes. In fact, your first maths teacher can make you love or hate maths for the rest of your life; depending on how they teach mathematics during your first few encounters with maths in primary school. I say primary (infants or junior) school as it’s literally make or break here. Anyone who does not make it in primary school may never make it! But only break. The subject knowledge gap will get wider every year that it may never be fully closed!
When people say, “I hate fractions”, “I don’t like maths” or “I’m not good at this subject”, my immediate response is, “You do not hate, you were made to hate it” or “You are not rubbish at it, you were not taught properly”. People just don’t hate something, a person or place. It’s their ‘experience’.
For instance, someone did something we dislike, then we quickly say, I don’t … that person. It’s not about the person but what (or how) they did or did not do.
Same for fractions, maths, or teaching in general. It’s how you were taught or not taught about it.
After all, we were born knowing nothing. It does not mean we were good at the things we now know and hate the ones we still don’t know or not good at.
That’s all.
It was in year 4 and 5 where I got hooked on everything algebra (another fundamental building block of mathematics) because we could have a competition to see who could best work out the optimal number of items (sweets and children stuff ☺) to buy from our pocket money to share among us friends.
In comparison, a friend of mine used to question, “Where in the world, will you use ‘x’ and ‘y’?”
You see, it’s all about understanding the usefulness and ‘uses’ (or applications) of something – a maths topic, tool, idea and so on.
There’s a saying in some cultures, “What you learn at young, benefits. Benefits and benefits. Forever”.
Which implies what you did not learn or did not learn properly at young, or start learning when you’re old, may never benefit or not benefit much as it seems like playing a catch-up game in life.
In short, most successful people are early outliers who started their business and careers when they were young. Being an outlier in education is much better with the help of supportive teachers and educators with a creative approach in mathematical subjects, particularly maths, physics and design & technology.
4. What advantage do you think your colourful and practical approach to fractions has on a child’s understanding of these concepts?
Children are visual learners. (Now, we all are – thanks to modern technologies, the Internet and social videos).
A child may not fully understand a cat unless they actually see a picture of it first. Hence, the reason why picture books exist. Fractions Visually are the equivalent of picture books for fractions. It’s a fraction and shape association.
Fractions Visually are conveniently illustrated with visual aids; basic shapes (colourful or shaded), images, kids characters and short stories on sharing.
Content is simplified, organised and logically ordered with clear, concise and easy to understand structure specifically designed to help KS1 and KS2 school children master basic maths fractions.
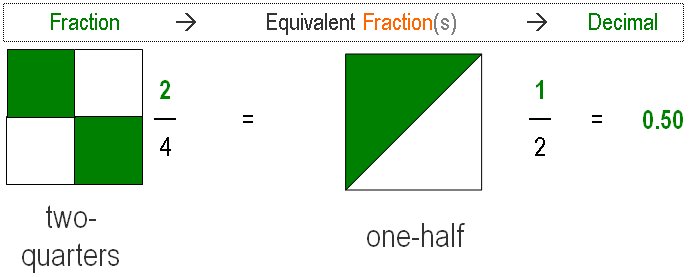
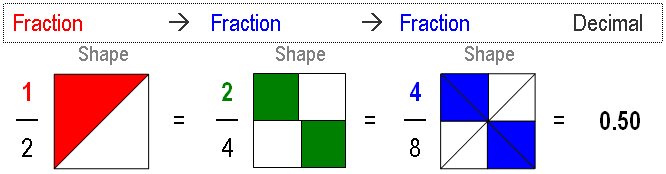
Every fraction is shown in 4 different ways:
- shape,
- fraction name,
- proper fraction and
- decimal fraction
each from nothing to whole.
Therefore, the child first sees the image of the fraction, then all the other information associated with that particular fraction. Similar to how children record an image of an animal and its name in their memory.
Fractions Visually cover all common fractions; halves, quarters, eighths, fifths, tenths, thirds, sixths and ninths – each from nothing to whole!
Visual fractions are grouped into similar, related families of fractions.
In short, visually simplifying the concept of understanding and adding maths fractions for children who think fractions are no fun and grown-ups who have never found the best visual resources to master basic maths fractions.
5. With your background in electrical engineering, would you say that teaching these basic maths concepts with this approach, that it might help grow interest in STEM careers in general?
I hope so. I think the STEM system, strategy and schemes are a bit decentralisation at the moment often with so many think tanks, special groups and agencies all competing in their specific interests and influence instead of the benefits of the public good and the system itself.
We’ll wait and see if and when it improves.
6. What do you think are the biggest advantages of using a tutor for your children?
I’m more familiar with working in schools and colleges.
The most important is finding the educational strengths and weaknesses of your child through observation such as gaps in their subject/s knowledge.
Then, to provide educational support specifically tailored to the child’s individual needs so that they can fully access the education curriculum and do well in school.
Not many schools have differentiated teaching and learning policy due to the limited resources available. As a result, some children will be left behind. And if there are any gaps in their educational progress, then that gap will only get wider and wider from primary school to secondary/sixth form and beyond.
7. What drew you to the world of educational tutoring and writing?
I think one event has just led to another.
First, I had very supportive teachers in school, who left a deep impression on my then very young mind.
I’m passionate about education (including lifelong learning) and I enjoy passing my expertise and knowledge to others in education and the community. Particularly children and young people to inspire them through learning so that they become excellent learners or educators and other professionals in other professions and industries.
In general, there is some satisfaction in leaving some useful knowledge for humankind before one dies and becomes bones and dust.
Secondly, during the high tech and semiconductor industry recession in late 2001/early 2002, many private investors and large organisations paused or stopped investing in business. Some of my friends and I were made redundant in 2003 due to company down-sizing and business acquisition by a big multinational organisation. I thought about self-employment and I once ran my own small firm in computer repairs and maintenance.
When replacing computers and their peripherals became cheaper than fixing them, I started accepting job contracts from engineering companies before finally moving into education.
Thirdly, working in education took me into writing as I had something useful to write about and share with other people; school children and adult learners.
Who knows where writing will lead me.
Fractions Visually is for children who think fractions are no fun and grown-ups who have never found the best visual resources to master basic maths fractions.
Ages 5-11, Year groups 1-6 and Key Stages 1-2.
Or internationally equivalents in primary curriculum (infants and junior schools).
Make sure to have a look at Fractions Visually
 Loading...
Loading...